PHÂN TÍCH THỐNG KÊ CÁC THỬ NGHIỆM VÀ ĐỊNH LƯỢNG SINH HỌC

13.10. PHÂN TÍCH THỐNG KÊ KẾT QUẢ ĐỊNH LƯỢNG SINH HỌC

1. Mở đầu

Chuyên luận này hướng dẫn cách bố trí thí nghiệm và phương pháp phân tích thống kê kết quả của các định lượng sinh học có trong Dược điển Việt Nam.

Có thể dùng kiểu bố trí thí nghiệm và cách tính toán kết quả khác với phương pháp mô tả trong chuyên luận này, miễn sao các phương pháp đó có độ tin cậy tương đương.

Phương pháp sinh học được dùng để định lượng các hợp chất hay chế phẩm mà hoạt lực của chúng không thể xác định một cách chính xác bằng các phương pháp phân tích Hóa - Lý. Nguyên tắc của phương pháp là so sánh chế phẩm cần định lượng với một chất chuẩn để xác định lượng chế phẩm cần định lượng cho cùng tác động sinh học với lượng biết trước, tính bằng đơn vị, của chất chuẩn. Để đảm bảo độ chính xác của kết quả định lượng, mọi thử nghiệm tiến hành với chế phẩm chuẩn và chế phẩm cần định lượng phải thực hiện đồng thời và trong cùng điều kiện thí nghiệm.

Định lượng sinh học luôn luôn mắc phải sai số ngẫu nhiên do tính biến thiên vốn có của đáp ứng sinh học, do đó nếu có thể, khi tính kết quả của mỗi định lượng phải tính sai số của định lượng, kể cả khi dùng phương pháp chính thức. Vì vậy, trong chuyên luận này có hướng dẫn các phương pháp bố trí thí nghiệm và cách tính sai số cho mỗi kiểu bố trí thí nghiệm tương ứng. Các phương pháp tính toán trình bày ở đây chỉ tính đến sai số ngẫu nhiên gây bởi chỉ thị sinh học và giả định rằng các sai số hệ thống, ví dụ sai số do cân, pha loãng, … là rất nhỏ và không ảnh hưởng đáng kể đến kết quả định lượng (do đó phải có biện pháp thích hợp để giảm sai số hệ thống đến mức có thể chấp nhận được). Trong mọi trường hợp, trước khi áp dụng một phương pháp thống kê bất kỳ, phải tiến hành định lượng sơ bộ một số lần thích hợp để bảo đảm chắc chắn tính khả dụng của phương pháp đó.

Độ chính xác của kết quả định lượng sinh học được xác định bởi các giới hạn tin cậy, còn gọi là khoảng tin cậy. Giới hạn tin cậy ở xác suất 95 % thường được sử dụng trong các định lượng sinh học, do đó cũng được chọn trong chuyên luận này. Khoảng tin cậy tính bằng các phương pháp toán thống kê giới thiệu ở đây có khả năng chứa hoạt lực thật của chế phẩm cần định lượng với xác suất 95 %. Một số chuyên luận Dược điển qui định giới hạn tin cậy phải không được vượt quá một ngưỡng nhất định, ví dụ phải nằm trong khoảng từ 95 % đến 105 % so với hoạt lực tính được, trong những trường hợp như vậy, có thể phải lặp lại định lượng hai hay nhiều lần để đạt được giới hạn tin cậy cho phép.

Các thuật ngữ dùng trong chuyên luận này được trình bày ở phần cuối của chuyên luận.

2. Ngẫu nhiên hóa

Sự chỉ định những liều khác nhau của chế phẩm chuẩn và chế phẩm cần định lượng cho các đơn vị thí nghiệm (ví dụ động vật thí nghiệm, ống nghiệm, …) phải được thực hiện một cách hoàn toàn ngẫu nhiên. Những điều kiện thí nghiệm khác, nếu không bắt buộc phải chuẩn hóa nhằm giảm chênh lệch đáp ứng sinh học giữa các đơn vị thí nghiệm (ví dụ chọn lựa cân nặng, tuổi của động vật thí nghiệm, điều kiện môi trường thí nghiệm, …), cũng phải lựa chọn càng ngẫu nhiên càng tốt. Chọn vị trí của chuồng nuôi động vật thí nghiệm trong phòng thí nghiệm, trình tự phân liều, … là những ví dụ cho các quá trình phải thực hiện một cách ngẫu nhiên.

Ngẫu nhiên hóa có thể thực hiện bằng cách ném xúc xắc, xào các lá bài có đánh số, dùng bảng số ngẫu nhiên hay các phần mềm vi tính thích hợp.

3. Các định lượng dựa trên đáp ứng định lượng

3.1. Mô hình thống kê

3.1.1. Nguyên tắc chung

Hai mô hình thống kê thường dùng trong các định lượng sinh học là mô hình đường thẳng song song và mô hình tỷ lệ độ dốc. Trong chuyên luận này chỉ giới thiệu mô hình đường thẳng song song, để tìm hiểu thêm về mô hình còn lại, xin tham khảo Dược điển Châu Âu IV hay các tài liệu thống kê khác.

Chỉ có thể áp dụng mô hình thống kê đường thẳng song song nếu định lượng hội đủ các điều kiện sau:

1) Các liều khác nhau của chế phẩm chuẩn và chế phẩm cần định lượng đã được chỉ định cho từng đơn vị thí nghiệm một cách ngẫu nhiên;

2) Các đáp ứng đo được của mỗi liều tuân theo phân phối chuẩn;

3) Độ lệch chuẩn của các đáp ứng trong mỗi nhóm xử lý của cả chế phẩm chuẩn và chế phẩm cần định lượng không khác nhau có ý nghĩa.

Sau khi tiến hành định lượng lặp lại nhiều lần, nhà phân tích phải kiểm tra các số liệu thu thập được bằng các phép kiểm tra thống kê thích hợp để đảm bảo định lượng thỏa mãn các điều kiện nói trên:

- Điều kiện 1 có thể thỏa mãn nếu thực hiện đúng theo các hướng dẫn trình bày ở mục 2 (Ngẫu nhiên hóa).

- Điều kiện 2 thường được chấp nhận là luôn luôn thỏa mãn trong thực tế. Trong những định lượng mà mỗi xử lý bao gồm một số đáp ứng lặp lại, một sự lệch nhỏ khỏi tính chuẩn sẽ không gây ảnh hưởng lớn đến kết quả.

- Kiểm tra điều kiện 3 thông qua việc kiểm tra tính đồng nhất của các phương sai, ví dụ bằng phép kiểm tra Bartlett hoặc phép kiểm tra Hartley (xem các ví dụ trong mục 3.2.8).

Nếu điều kiện 2 và/hoặc điều kiện 3 không thỏa mãn, thay đáp ứng y bằng ln(y), hay y² ‎‎có thể cho kết quả tốt.

Phép biến đổi y thành ln(y) rất hữu ích trong trường hợp tính đồng nhất của các phương sai không thỏa mãn. Phép biến đổi này cũng giúp cải thiện tính chuẩn nếu phân phối bị lệch về bên phải.

Biến đổi y thành thường được dùng khi các quan sát tuân theo phân phối Poisson, ví dụ khi các quan sát thu được bằng phương pháp đếm.

3.1.2. Các định lượng thường nhật

Trong các định lượng thường nhật, rất khó kiểm tra một cách hệ thống các điều kiện lý thuyết mô tả ở mục 3.1.1, bởi vì trong thực tế số quan sát của các định lượng thường nhỏ do đó ảnh hưởng đến độ nhạy của các phép kiểm tra thống kê. Tuy nhiên, trong những định lượng cân xứng (là những định lượng có số liều của chế phẩm chuẩn bằng với số liều của chế phẩm cần định lượng, ví dụ: định lượng 2 + 2, 3 + 3, …) một sự lệch nhỏ khỏi tính chuẩn hay khỏi tính đồng nhất của phương sai không ảnh hưởng lớn đến kết quả định lượng. Do đó, chỉ cần kiểm tra lại các điều kiện lý thuyết nói trên khi một loạt các định lượng liên tục không thỏa mãn phép kiểm tra tính có giá trị (xem mục 3.2.4).

Ngoài 3 điều kiện lý thuyết đã nói trên, mô hình thống kê đường thẳng song song còn yêu cầu mỗi định lượng phải thỏa mãn 2 điều kiện sau:

4) Đường biểu diễn mối quan hệ giữa logarithm liều và đáp ứng phải tuyến tính trong khoảng liều đã dùng trong định lượng.

5) Đường thẳng ln(liều) – đáp ứng của chế phẩm cần định lượng phải song song với đường ln(liều) – đáp ứng của chế phẩm chuẩn.

Chỉ có thể kiểm tra điều kiện 4 nếu định lượng được tiến hành với ít nhất 3 nồng độ pha loãng của mỗi chế phẩm (định lượng 3 liều hay lớn hơn). Tuy nhiên, nếu tính tuyến tính của đường logarithm liều – đáp ứng, trong một khoảng liều nhất định, đã được chứng minh bởi một số lượng đủ lớn các định lượng có 3 liều trở lên, có thể tiến hành định lượng chỉ với 2 liều của mỗi chế phẩm (định lượng 2 liều) trong các định lượng hàng ngày, dùng khoảng liều đã cho.

Trước khi tính hoạt lực và các giới hạn tin cậy, cần phải tiến hành phân tích phương sai để kiểm tra xem định lượng có đáp ứng các điều kiện 4 và 5 hay không.

Các định lượng dựa trên mô hình thống kê đường thẳng song song được trình bày trong mục 3.2.

Nếu có bất cứ điều kiện nào trong 5 điều kiện nói trên không thỏa mãn, các phương pháp tính toán giới thiệu ở đây sẽ không có giá trị. Khi đó, phải tiến hành rà soát lại các kỹ thuật định lượng để tìm ra nguyên nhân.

Nếu các phép kiểm tra thống kê cho thấy một hay một vài điều kiện trong 5 điều kiện nói trên không thỏa mãn trong một số định lượng hàng ngày, không được chuyển ngay sang một phép biến đổi khác trừ khi có đủ bằng chứng rằng nguyên nhân gây ra hiện tượng đó không phải do ngẫu nhiên mà là kết quả của một sự thay đổi có hệ thống của các điều kiện thí nghiệm. Trước khi áp dụng một phép biến đổi mới vào các định lượng thường nhật phải lặp lại các phép kiểm tra thống kê đã trình bày ở mục 3.1.1.

Để thu được một kết quả định lượng đáng tin cậy, có thể phải tiến hành một vài định lượng độc lập, sau đó phối hợp các kết quả định lượng lại với nhau (xem mục 4).

Nhằm mục đích kiểm soát chất lượng của các định lượng hàng ngày, nên ghi chép lại các kết quả tính độ dốc hồi qui và sai số dư dưới dạng biểu đồ kiểm tra.

Nếu sai số dư lớn một cách bất thường, nguyên nhân đầu tiên phải nghĩ đến là sai sót trong kỹ thuật định lượng. Nếu các khảo sát khẳng định điều đó là đúng, phải lặp lại định lượng. Sai số dư cũng có thể rất lớn nếu trong dãy số liệu đo có một giá trị bất thường. Chỉ được loại bỏ giá trị nghi ngờ là bất thường nếu phép kiểm tra thống kê thích hợp cho thấy giá trị đó khác có ý nghĩa với các giá trị còn lại.

Sai số dư có thể nhỏ bất thường trong một số định lượng hàng ngày và làm cho các tỷ số F vượt quá giá trị tới hạn. Trong những trường hợp như vậy, có thể thay sai số dư tính được của định lượng bằng sai số dư trung bình của các định lượng trước đó trong biểu đồ kiểm tra.

3.1.3. Cách tính toán và một số hạn chế

Dưới đây là 3 hạn chế áp đặt cho mỗi định lượng nhằm làm đơn giản hóa các công thức tính toán và làm tăng độ chính xác của định lượng:

a) số nồng độ pha loãng của mỗi chế phẩm trong một định lượng phải bằng nhau;

b) tỷ lệ giữa các liều kế tiếp nhau phải là một hằng số đối với tất cả các xử lý trong một định lượng, ví dụ: S₂/S₁ = S₃/S₂ = … = Z₃/Z₂;

c) số các đơn vị thí nghiệm của mỗi xử lý phải bằng nhau.

Các công thức tính toán áp dụng cho những định lượng có bố trí thí nghiệm tuân thủ đúng 3 hạn chế nêu trên được giới thiệu ở mục 3.2. Đối với các định lượng có bố trí thí nghiệm không tuân theo các hạn chế đã nêu các công thức tính toán sẽ rất phức tạp và không được giới thiệu trong chuyên luận này.

Trong mục 3.2.8 có trình bày một số ví dụ để minh họa cho phần lý thuyết thống kê. Có thể dùng các số liệu trong các ví dụ đó để kiểm tra các phần mềm dùng trong phân tích thống kê kết quả định lượng sinh học.

3.2. Mô hình đường thẳng song song

3.2.1. Giới thiệu

Mô hình đường thẳng song song dựa trên quan hệ tuyến tính giữa đáp ứng Y và logarithm X của liều D.

Y = a + bX

Trong đó:

Y = đáp ứng mong đợi.

X = ln(liều) = ln(D).

a và b là các hằng số.

Mô hình đường thẳng song song có thể được minh họa bởi đồ thị trong hình 3.2.1.-I. Trên đồ thị, trục hoành biểu diễn các logarithm liều, trục tung biễu diễn các đáp ứng đo được. Các đáp ứng riêng của mỗi xử lý được biểu thị bằng các chấm đen. Hai đường trên đồ thị biểu diễn mối quan hệ giữa logarithm liều và đáp ứng đo được của chế phẩm chuẩn và chế phẩm cần định lượng.

Từ trục tung kẻ một đường thẳng bất kỳ song song với trục hoành, cắt hai đường ln(liều) – đáp ứng tại hai điểm. Giá trị tương ứng của hai diểm này trên trục hoành là Z_S và Z_U, đây là hai nồng độ của chế phẩm chuẩn và chế phẩm cần định lượng cho cùng đáp ứng sinh học. Vì khi pha các dung dịch thử của chế phẩm chuẩn và chế phẩm cần định lượng ta đã giả định Z_S = Z_U, do đó, đoạn thẳng ln(Z_S) – ln(Z_U) là chênh lệch giữa nồng độ thật và nồng độ giả định của chế phẩm cần định lượng trên thang logarithm. Đó cũng chính là logarithm tỷ lệ hoạt lực giữa chế phẩm chuẩn và chế phẩm cần định lượng.

Vì Z_S đã biết, ta có thể tính được Z_U.

Mẫu thử

Hình 3.2.1.-I. – Mô hình đường thẳng song song của một định lượng 3 + 3.

Chú ý: logarithm tự nhiên ln (hay log_e) được sử dụng xuyên suốt trong chuyên luận này, do đó, antilogarithm tương đương với e^x. Tuy nhiên, nếu muốn, hoàn toàn có thể dùng logarithm cơ số 10 ( hay log₁₀) thay cho ln, khi đó, antilogarithm tương ứng với 10^x.

Trong một định lượng, nếu đoạn thẳng ln(Z_S) – ln(Z_U) càng nhỏ, tức là nếu hoạt lực giả định của chế phẩm cần định lượng càng gần với hoạt lực thật của nó, kết quả định lượng sẽ càng chính xác.

3.2.2. Bố trí thí nghiệm

Các định lượng sinh học có thể được bố trí theo một số cách khác nhau như trình bày dưới đây.

3.2.2.1. Bố trí thí nghiệm ngẫu nhiên hoàn toàn

Nếu toàn bộ các đơn vị thí nghiệm (động vật, ống nghiệm,…) tương đối đồng nhất, việc chỉ định các đơn vị thí nghiệm cho các xử lý khác nhau phải được tiến hành một cách ngẫu nhiên, ví dụ dùng bảng hoán vị ngẫu nhiên.

Nếu chia các đơn vị thí nghiệm thành các phân nhóm, ví dụ theo vị trí vật lý hay ngày thí nghiệm, mà các đáp ứng đo được có độ phân tán nhỏ hơn, ta có thể tăng độ chính xác của định lượng bằng cách áp dụng một số hạn chế trong cách bố trí thí nghiệm. Sự sắp xếp các đơn vị thí nghiệm theo các hạn chế đó cho phép loại bỏ một số nguồn gây sai số không liên quan.

3.2.2.2. Bố trí thí nghiệm ngẫu nhiên theo khối

Trong kiểu bố trí thí nghiệm này, có thể giảm sai số của định lượng bằng cách tách độ phân tán giữa các khối, ví dụ độ phân tán giữa các hộp Petri trong định lượng vi sinh vật bằng phương pháp khuếch tán, khỏi sai số toàn phần. Bố trí thí nghiệm ngẫu nhiên theo khối đòi hỏi mỗi khối phải có số xử lý bằng nhau và chỉ thích hợp nếu khối (ví dụ hộp Petri) đủ lớn để có thể chứa tất cả các xử lý của định lượng.

Bảng 3.2.3.-V trình bày công thức tính toán áp dụng cho các định lượng có bố trí thí nghiệm ngẫu nhiên theo khối, trong đó mỗi xử lý chỉ xuất hiện một lần duy nhất trong mỗi khối (Bố trí thí nghiệm ngẫu nhiên theo khối không lặp). Ví dụ minh họa cho kiểu bố trí thí nghiệm này được trình bày trong ví dụ 3.2.8.2.

3.2.2.3. Bố trí thí nghiệm hình vuông Latin

Kiểu bố trí thí nghiệm này thích hợp với những định lượng mà đáp ứng chịu ảnh hưởng của 2 nguồn gây sai số khác nhau, trong đó mỗi nguồn sai số có k mức hay k vị trí khác nhau. Ví dụ, trong định lượng kháng sinh bằng phương pháp khuếch tán các xử lý có thể được sắp thành dãy trên một khay lớn, mỗi xử lý chỉ xuất hiện một lần duy nhất trong mỗi hàng và mỗi cột. Chỉ có thể áp dụng kiểu bố trí thí nghiệm hình vuông Latin khi số hàng bằng với số cột và số xử lý của mỗi chế phẩm phải bằng nhau.

Các đáp ứng đo được được ghi vào một bảng hình vuông gọi là hình vuông Latin. Sai số do chênh lệch đáp ứng giữa k hàng và giữa k cột sẽ được tách khỏi sai số toàn phần, do đó làm giảm sai số của định lượng.

Bảng 3.2.3.-V trình bày công thức tính toán áp dụng cho các định lượng có bố trí thí nghiệm hình vuông Latin, trong đó mỗi xử lý chỉ xuất hiện một lần duy nhất trong mỗi hàng và mỗi cột. Ví dụ minh họa cho kiểu bố trí thí nghiệm này được trình bày trong ví dụ 3.2.8.3.

3.2.2.4. Bố trí thí nghiệm chéo

Kiểu bố trí thí nghiệm này được áp dụng trong trường hợp các đơn vị thí nghiệm có thể chia thành các khối khác nhau, nhưng mỗi khối chỉ có thể nhận hai xử lý, ví dụ một khối chỉ gồm một đơn vị thí nghiệm được thử hai lần vào hai thời điểm khác nhau. Mục đích của kiểu bố trí chéo là làm tăng độ chính xác của định lượng bằng cách loại trừ ảnh hưởng do sự khác biệt giữa các đơn vị thí nghiệm. Nếu định lượng tiến hành với 2 liều của chế phẩm chuẩn và chế phẩm cần định lượng, ta có kiểu thí nghiệm chéo đôi.

Bảng 3.2.2.-I. – Cách sắp xếp các liều trong bố trí thí nghiệm chéo

Nhóm các đơn vị thí nghiệm	Giai đoạn I	Giai đoạn II
1	s₁	u₂
2	s₂	u₁
3	u₁	s₂
4	u₂	s₁

Trong thí nghiệm chéo đôi, định lượng được chia thành hai giai đoạn, mỗi giai đoạn tiến hành vào những thời điểm khác nhau. Các đơn vị thí nghiệm được chia thành bốn nhóm, mỗi nhóm nhận một trong bốn xử lý ở giai đoạn đầu của thí nghiệm. Đơn vị nhận một chế phẩm trong giai đoạn đầu sẽ nhận chế phẩm khác trong giai đoạn sau, các đơn vị nhận liều thấp trong giai đoạn đầu sẽ nhận liều cao trong giai đoạn sau. Cách sắp xếp các liều cho ở Bảng 3.2.2.-I. Ví dụ minh họa cho kiểu bố trí thí nghiệm này được trình bày trong ví dụ 3.2.8.4.

3.2.3. Phân tích phương sai

Mục này trình bày các công thức cần thiết để phân tích phương sai. Người đọc sẽ dễ hiểu hơn nếu tham khảo thêm các ví dụ ở mục 3.2.8 và các ký hiệu thuật ngữ ở mục 6.

Các công thức trình bày ở đây có thể áp dụng cho các định lượng đối xứng trong đó một hay nhiều chế phẩm cần thử (U, …, Z) được so sánh với cùng một chế phẩm chuẩn S, với điều kiện định lượng phải đáp ứng được các điều kiện sau: 1) tỷ lệ giữa các liều kế tiếp nhau của tất cả các chế phẩm phải là một hằng số, 2) số xử lý của mỗi chế phẩm và 3) số đơn vị thí nghiệm trong mỗi xử lý phải bằng nhau (xem mục 3.1.3).

Ngoại trừ một vài khác biệt nhỏ trong cách tính sai số dư, phương pháp phân tích các số liệu của mỗi định lượng sinh học về cơ bản là giống nhau đối với các kiểu bố trí thí nghiệm ngẫu nhiên hoàn toàn, ngẫu nhiên theo khối và hình vuông Latin. Bố trí thí nghiệm chéo có công thức tính hoàn toàn khác và do đó được trình bày trực tiếp trong ví dụ 3.2.8.4.

Để chuẩn bị số liệu cho phân tích phương sai, đầu tiên phải tính tổng đáp ứng của mỗi liều, tổng đáp ứng và tương phản tuyến tính (linear contrast) của mỗi chế phẩm, đối với các định lượng có nhiều hơn hai liều của mỗi chế phẩm, cần tính thêm tương phản bậc hai (quadratic contrast). Các Bảng 3.2.3.-I, 3.2.3.-II và 3.2.3.-III trình bày các công thức tính đó.

Bảng 3.2.3.-I. – Công thức tính toán cho các định lượng mỗi chế phẩm có hai liều

	Chế phẩm chuẩn S	Chế phẩm thử thứ nhất U	Chế phẩm thử thứ (h – 1) Z
Tổng đáp ứng của liều thấp	S₁	U₁	Z₁
Tổng đáp ứng của liều cao	S₂	U₂	Z₂
Tổng đáp ứng của chế phẩm	S₁ + S₂ = S	U₁ + U₂ = U	Z₁ + Z₂ = Z
Tương phản tuyến tính	S₂ – S₁ = L_S	U₂ – U₁ = L_U	Z₂ – Z₁ = L_Z

Bảng 3.2.3.-II. – Công thức tính toán cho các định lượng mỗi chế phẩm có ba liều

	Chế phẩm chuẩn S	Chế phẩm thử thứ nhất U	Chế phẩm thử thứ (h – 1) Z
Tổng đáp ứng của liều thấp	S₁	U₁	Z₁
Tổng đáp ứng của liều trung bình	S₂	U₂	Z₂
Tổng đáp ứng của liều cao	S₃	U₃	Z₃
Tổng đáp ứng của chế phẩm	S₁ + S₂ + S₃ = S	U₁ + U₂ + U₃ = U	Z₁ + Z₂ + Z₃ = Z
Tương phản tuyến tính	S₃ – S₁ = L_S	U₃ – U₁ = L_U	Z₃ – Z₁ = L_Z
Tương phản bậc hai	S₁ – 2S₂ + S₃ = Q_S	U₁ – 2U₂ + U₃ = Q_U	Z₁ – 2Z₂ + Z₃ = Q_Z

Bảng 3.2.3.-III. – Công thức tính toán cho các định lượng mỗi chế phẩm có bốn liều

	Chế phẩm chuẩn S	Chế phẩm thử thứ nhất U	Chế phẩm thử thứ (h – 1) Z
Tổng đáp ứng của liều thấp nhất	S₁	U₁	Z₁
Tổng đáp ứng của liều thứ hai	S₂	U₂	Z₂
Tổng đáp ứng của liều thứ ba	S₃	U₃	Z₃
Tổng đáp ứng của liều cao nhất	S₄	U₄	Z₄
Tổng đáp ứng của chế phẩm	S₁ + S₂ + S₃ + S₄ = S	U₁ + U₂ + U₃ + U₄ = U	Z₁ + Z₂ + Z₃ + Z₄ = Z
Tương phản tuyến tính	3S₄ + S₃ – S₂ – 3S₁ = L_S	3U₄ + U₃ – U₂ – 3U₁ = L_U	3Z₄ + Z₃ – Z₂ – 3Z₁ = L_Z
Tương phản bậc hai	S₁- S₂ - S₃ + S₄ = Q_S	U₁ – U₂ – U₃ + U₄ = Q_U	Z₁ – Z₂ – Z₃ + Z₄ = Q_Z
Tương phản bậc ba	3S₂ – S₁ + S₄ – 3S₃ = J_S	3U₂ – U₁ + U₄ – 3U₃ = J_U	3Z₂ – Z₁ + Z₄ – 3Z₃ = J_Z

Trong bước kế tiếp, sai số toàn phần của định lượng, còn gọi là sai số chung, được phân tích thành các sai số riêng phần như trình bày ở Bảng 3.2.3.-IV, các tổng các bình phương được tính từ các giá trị thu được ở các Bảng 3.2.3.-I, 3.2.3.-II và 3.2.3.-III.

Bảng 3.2.3.-IV Kiểm tra tính có giá trị của định lượng

Nguồn gây sai số	Bậc tự do (f)	Tổng các bình phương
Nguồn gây sai số	Bậc tự do (f)	2 liều/chế phẩm	3 liều/chế phẩm	4 liều/chế phẩm
Chế phẩm	h - 1
Hồi qui tuyến tính	1
Tính không song song	h - 1
Tính không tuyến tính (Độ cong)	h (3 liều) 2h (4 liều)	-

Tính sai số dư (residual error) bằng cách lấy sai số toàn phần của định lượng trừ đi các sai số riêng của các nguồn gây sai số khác nhau (Bảng 3.2.3.-V), nguồn gây sai số có thể nhận dạng được khác nhau tùy theo kiểu bố trí thí nghiệm. Trong Bảng 3.2.3.-V, ∑y² là tổng của bình phương của tất cả các đáp ứng đo được của mỗi định lượng, K là số hiệu chỉnh:

Kết thúc phân tích phương sai bằng cách chia các tổng các bình phương tính được từ Bảng 3.2.3.-IV cho bậc tự do tương ứng để được các bình phương trung bình.

Bình phương trung bình của sai số dư cũng được tính theo cách tương tự, dùng số liệu tương ứng ở Bảng 3.2.3.-V.

Bình phương trung bình của mỗi biến số cần kiểm tra sẽ được biểu diễn dưới dạng một tỷ số với sai số dư s², gọi là tỷ số F. Đánh giá mức ý nghĩa của các tỷ số F bằng cách so sánh F tính được (viết tắt là F_cal.) với giá trị F tới hạn (viết tắt là F_crit.) tra từ Bảng 3.2.4.-I hay bằng cách dùng các phần mềm vi tính thích hợp. Nếu dùng bảng tra cứu, đọc F_crit.từ Bảng 3.2.4.-I tại giao điểm giữa cột tương ứng với bậc tự do của bình phương trung bình của biến số cần kiểm tra (f₁) và hàng tương ứng với bậc tự do của s² (f₂). Biến số cần kiểm tra được coi là có ý nghĩa nếu F_cal.> F_crit.ở xác suất P = 0,05 hay rất có ý nghĩa nếu F_cal.> F_crit.ở xác suất P = 0,01.

Bảng 3.2.3.-V. – Tính sai số dư

Nguồn gây sai số	Bậc tự do (f)	Tổng các bình phương
Nguồn gây sai số	Bậc tự do (f)	Ngẫu nhiên hoàn toàn	Ngẫu nhiên theo khối	Hình vuông Latin
Giữa các xử lý	k – 1
Giữa các khối (hàng)	n – 1	-
Giữa các khối (cột)	n – 1	-	-
Sai số dư	Hiệu số	*	*	*
Sai số toàn phần	N – 1

* Lấy sai số toàn phần trừ đi các tổng các bình phương tương ứng của mỗi phương pháp bố trí thí nghiệm.

3.2.4. Kiểm tra tính có giá trị của định lượng

Một định lượng được coi là có giá trị thống kê (statistically valid) nếu:

1) Đại lượng hồi qui tuyến tính rất có ý nghĩa, F_cal. > F_crit. ở xác suất P = 0,01 (P < 0,01), chứng tỏ độ dốc của đường ln(liều) – đáp ứng rất khác 0.

2) Đại lượng không tuyến tính (non-linearity) phải không có ý nghĩa, F_cal. < F_crit. ở xác suất 0,05 (P > 0,05), chứng tỏ thoả mãn điều kiện 4, tức là các đường ln(liều) – đáp ứng của chế phẩm chuẩn S và các chế phẩm thử (U,…,Z) thẳng.

3) Đại lượng không song song (non-parallelism) phải không có ý nghĩa, F_cal. < F_crit. ở xác suất 0,05 (P > 0,05), chứng tỏ định lượng đáp ứng điều kiện 5, hay nói cách khác các đường ln(liều) – đáp ứng của các chế phẩm thử (U,…,Z) song song với đường ln(liều) – đáp ứng của chế phẩm chuẩn S.

Nếu đại lượng không song song có ý nghĩa trong một định lượng có h chế phẩm, kể cả chế phẩm chuẩn, một trong số các chế phẩm cần thử có thể có độ dốc của đường ln(liều) – đáp ứng khác với các chế phẩm còn lại. Tính t’ (phép kiểm tra Dunnett) của mỗi chế phẩm cần định lượng (U, …, Z) theo công thức:

(3.2.4.-I)

Đối với các định lượng có bốn liều của mỗi chế phẩm, tính t’ theo công thức:

So sánh mỗi t’ tính được với giá trị tới hạn đọc từ Bảng 3.2.4.-II, với f₁ = h – 1, f₂ là bậc tự do của s². Nếu t’ có ý nghĩa với một chế phẩm bất kỳ, loại bỏ tất cả các số liệu liên quan đến chế phẩm đó và lặp lại từ đầu phép kiểm tra tính có giá trị với các chế phẩm còn lại.

Sai số do chế phẩm không được dùng để kiểm tra tính có giá trị của định lượng, tuy nhiên, trong những định lượng mà sai số dư lớn một cách bất thường và tỷ số F của nguồn gây sai số do chế phẩm rất có ý nghĩa, hoạt lực giả định của chế phẩm cần định lượng rất khác với hoạt lực thật của nó, cần phải lặp lại định lượng dùng hoạt lực tính được làm hoạt lực giả định.

Bảng 3.2.4.-I. – Mức ý nghĩa của tỷ số F

		f₁
		1	2	3	4	5	6	7	8	20	∞
f₂	12	4,75	3,89	3,49	3,26	3,11	3,00	2,91	2,85	2,54	2,30
		9,33	6,93	5,95	5,41	5,06	4,82	4,64	4,50	3,86	3,36
	15	4,54	3,68	3,29	3,06	2,90	2,79	2,71	2,64	2,33	2,07
		8,68	6,36	5,42	4,89	4,56	4,32	4,14	4,00	3,37	2,87
	20	4,35	3,49	3,10	2,87	2,71	2,60	2,51	2,45	2,12	1,84
		8,10	5,85	4,94	4,43	4,10	3,87	3,70	3,56	2,94	2,42
	25	4,24	3,39	2,99	2,76	2,60	2,49	2,40	2,34	2,01	1,71
		7,77	5,57	4,68	4,18	3,85	3,63	3,46	3,32	2,70	2,17
	30	4,17	3,32	2,92	2,69	2,53	2,42	2,33	2,27	1,93	1,62
		7,56	5,39	4,51	4,02	3,70	3,47	3,30	3,17	2,55	2,01
	40	4,08	3,23	2,84	2,61	2,45	2,34	2,25	2,18	1,84	1,51
		7,31	5,18	4,31	3,83	3,51	3,29	3,12	2,99	2,37	1,80
	60	4,00	3,15	2,76	2,53	2,37	2,25	2,17	2,10	1,75	1,39
		7,08	4,98	4,13	3,65	3,34	3,12	2,95	2,82	2,20	1,60
	∞	3,84	3,00	2,60	2,37	2,21	2,10	2,01	1,94	1,57	1,00
		6,63	4,61	3,78	3,32	3,02	2,80	2,64	2,51	1,88	1,00
* Nếu F tính được > F tới hạn, biến số cần kiểm tra được coi là có ý nghĩa (dòng trên, p = 0,05), hay rất có ý nghĩa (dòng dưới, p = 0,01). f₁ là bậc tự do của tử số, f2 là bậc tự do của mẫu số.

Bảng 3.2.4.-II. – Mức ý nghĩa của t’

f₁ = (h – 1) = số chế phẩm cần định lượng
f₂	1	2	3	4	5	6	7	8	9
5	2,57	3,03	3,29	3,48	3,62	3,73	3,82	3,90	3,97
6	2,45	2,86	3,10	3,26	3,39	3,49	3,57	3,64	3,71
7	2,36	2,75	2,97	3,12	3,24	3,33	3,41	3,47	3,53
8	2,31	2,67	2,88	3,02	3,13	3,22	3,29	3,35	3,41
9	2,26	2,61	2,81	2,95	3,05	3,14	3,20	3,26	3,32
10	2,23	2,57	2,76	2,89	2,99	3,07	3,14	3,19	3,24
11	2,20	2,53	2,72	2,84	2,94	3,02	3,08	3,14	3,19
12	2,18	2,50	2,68	2,81	2,90	2,98	3,04	3,09	3,14
13	2,16	2,48	2,65	2,78	2,87	2,94	3,00	3,06	3,10
14	2,14	2,46	2,63	2,75	2,84	2,91	2,97	3,02	3,07
15	2,13	2,44	2,61	2,73	2,82	2,89	2,95	3,00	3,04
16	2,12	2,42	2,59	2,71	2,80	2,87	2,92	2,97	3,02
17	2,11	2,41	2,58	2,69	2,78	2,85	2,90	2,95	3,00
18	2,10	2,40	2,56	2,68	2,76	2,83	2,89	2,94	2,98
19	2,09	2,39	2,55	2,66	2,75	2,81	2,87	2,92	2,96
20	2,09	2,38	2,54	2,65	2,73	2,80	2,86	2,90	2,95
24	2,06	2,35	2,51	2,61	2,70	2,76	2,81	2,86	2,90
30	2,04	2,32	2,47	2,58	2,66	2,72	2,77	2,82	2,86
40	2,02	2,29	2,44	2,54	2,62	2,68	2,73	2,77	2,81
60	2,00	2,27	2,41	2,51	2,58	2,64	2,69	2,73	2,77
120	1,98	2,24	2,38	2,47	2,55	2,60	2,65	2,69	2,73
∞	1,96	2,21	2,35	2,44	2,51	2,57	2,61	2,65	2,69

Nếu định lượng thỏa mãn các phép kiểm tra tính có giá trị, hay nói cách khác, định lượng có giá trị thống kê, có thể tiếp tục tính hoạt lực và các giới hạn tin cậy bằng các phương pháp mô tả trong mục kế tiếp.

3.2.5. Tính hoạt lực và các giới hạn tin cậy

Để tính hoạt lực và các giới hạn tin cậy, trước hết phải tính đáp ứng trung bình của mỗi chế phẩm :

(3.2.5.-1)

Tiến hành tương tự như vậy với các chế phẩm khác.

Gọi I là khoảng cách giữa ln các liều kế tiếp nhau của một chế phẩm bất kỳ (I là hằng số trong một định lượng), ví dụ I = ln(S₂) – ln(S₁), độ dốc chung (b) của một định lượng bao gồm h chế phẩm, mỗi chế phẩm có d liều khác nhau được tính theo công thức:

(3.2.5.-2)

Đối với các định lượng mỗi chế phẩm có bốn liều, tính b theo công thức:

ln(tỷ lệ hoạt lực) của chế phẩm cần định lượng U được tính theo công thức:

(3.2.5.-3)

Gọi A_U là hoạt lực giả định của chế phẩm U, logarithm hoạt lực của U (M_U) sẽ bằng:

(3.2.5.-4)

Hoạt lực tính được là ước lượng của hoạt lực thật của chế phẩm cần định lượng. Các giới hạn tin cậy của hoạt lực tính được là khoảng có khả năng chứa hoạt lực thật của chế phẩm cần định lượng với xác suất 95 %. Logarithm của các giới hạn tin cậy được tính theo công thức sau:

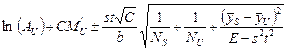(3.2.5.-5)

với: (3.2.5.-6)

E là giá trị tính được từ Bảng 3.2.3.-IV, tính s² bằng cách chia tổng các bình phương của biến số sai số dư trong Bảng 3.2.5.-V cho bậc tự do tương ứng của nó, t là giá trị đọc được từ Bảng 5.1 với xác suất P = 0,95 và f là bậc tự do của s².

Trong những định lượng đối xứng, công thức tính các giới hạn tin cậy có thể đơn giản hóa thành:

(3.2.5.-7)

với:

C là tiêu chuẩn đánh giá ý nghĩa của đường hồi qui, trong một định lượng có độ dốc đạt yêu cầu giá trị của C rất gần với 1. Nếu C < 0 hồi qui tuyến tính không có ý nghĩa.

Tính hoạt lực của chế phẩm U (R_U) và các giới hạn tin cậy của nó bằng cách lấy antilogarithm các giá trị tính được từ các công thức 3.2.5.-4 và 3.2.5.-7.

(3.2.5.-8)

(3.2.5.-9)

(3.2.5.-10)

FL_U là giới hạn tin cậy trên và FL_L là giới hạn tin cậy dưới của hoạt lực tính được R_U.

Nếu nồng độ dung dịch gốc của chế phẩm chuẩn và các chế phẩm thử không hoàn toàn giống nhau, phải hiệu chỉnh hoạt lực tính được và các giới hạn tin cậy với một hệ số, gọi là hệ số hiệu chỉnh (xem ví dụ 3.2.8.3). Hệ số hiệu chỉnh là tỷ số giữa nồng độ dung dịch gốc của chất chuẩn và nồng độ dung dịch gốc của mỗi chế cần định lượng.

3.2.6. Các giá trị bị mất

Trong những định lượng đối xứng, một sự cố ngẫu nhiên có thể dẫn đến việc mất một hay nhiều giá trị đo, ví dụ động vật thí nghiệm chết, vòng vô khuẩn bị méo không đo được, … Nếu sự cố xảy ra không liên quan đến thành phần của chế phẩm cần thử, vẫn có thể tính được kết quả định lượng một cách chính xác, tuy nhiên khi đó các công thức tính toán sẽ trở nên rất phức tạp. Để có thể tiếp tục dùng các công thức tính toán đơn giản của bố trí thí nghiệm đối xứng, có thể phục hồi tính đối xứng của định lượng bằng một trong hai cách sau:

1) Nếu số đáp ứng của mỗi xử lý đủ lớn, giảm số đáp ứng trong các xử lý có số đáp ứng lớn hơn cho đến khi số đáp ứng của tất cả các xử lý bằng nhau. Nếu động vật thí nghiệm đã được chỉ định một cách ngẫu nhiên cho mỗi xử lý, bỏ một hay vài đáp ứng, được chọn ngẫu nhiên, từ các xử lý có số đáp ứng lớn sẽ làm cho định lượng trở thành đối xứng. Đối với các định lượng bố trí thí nghiệm theo kiểu ngẫu nhiên theo khối, cách đơn giản nhất là bỏ tất cả các đáp ứng của khối có giá trị bị mất. Ví dụ, chỉ giữ lại kết quả đo của các hộp Petri có đủ 6 vòng vô khuẩn trong định lượng kháng sinh 3 + 3 bằng phương pháp khuếch tán, dùng hộp Petri.

2) Thay các giá trị bị mất bằng các giá trị tính được từ những giá trị còn lại. Công thức tính các giá trị mất được trình bày ở bên dưới, bậc tự do của sai số toàn phần và sai số dư sẽ phải giảm đi một đơn vị cho mỗi giá trị bị mất. Cần nhớ rằng đây chỉ là phương pháp gần đúng, phương pháp chính xác luôn luôn cho kết quả đáng tin cậy hơn.

Nếu có nhiều quan sát bị mất, thay tất cả các giá trị bị mất, trừ một quan sát, bằng các giá trị ước lượng thô và dùng công thức thích hợp để tính giá trị của quan sát đó dựa trên các giá trị còn lại, kể cả các giá trị ước lượng thô. Thay quan sát bị mất bằng giá trị vừa tính được. Tiếp tục tính theo cách trên với giá trị ước lượng thô thứ nhất … Sau khi đã thay thế tất cả các quan sát bị mất, lặp lại từ đầu chu trình tính toán cho đến khi hai chu trình kế tiếp nhau cho cùng kết quả.

Kết quả phân tích chỉ được chấp nhận nếu số các giá trị thay thế tương đối nhỏ (nhỏ hơn 5 %) so với tổng số đáp ứng của toàn bộ định lượng. Cần đặc biệt thận trọng trong trường hợp các giá trị bị mất có khuynh hướng tập trung trong một xử lý hay một khối nhất định.

Bố trí thí nghiệm ngẫu nhiên hoàn toàn

Trong kiểu bố trí thí nghiệm ngẫu nhiên hoàn toàn, thay giá trị bị mất bằng trung bình số học của các đáp ứng khác trong cùng xử lý.

Bố trí thí nghiệm ngẫu nhiên theo khối

Giá trị bị mất (y’) được tính bằng công thức:

(3.2.6.-1)

Trong đó B’ là tổng đáp ứng của khối chứa giá trị bị mất, T’ là tổng đáp ứng của xử lý chứa giá trị bị mất, G’ là tổng tất cả các đáp ứng còn lại trong định lượng.

Để minh họa, giả sử giá trị của u₁ trong khối thứ nhất (trong trường hợp này là hàng hay hộp Petri) ở ví dụ 3.2.8.2, Bảng 3.2.8.2.-II bị mất (u₁ = 174). Với:

B’ = 1.050

T’ = 869

G’ = 7.189

k = 6

n = 6

y’ = 173. Dùng giá trị tính được 173 thay cho đáp ứng của u₁ trong hộp số 1 của Bảng 3.2.8.2.-II và tiếp tục tính toán như trình bày trong ví dụ 3.2.8.2 nhưng với bậc tự do của sai số toàn phần là 34, và bậc tự do của sai số dư là 24.

Bố trí thí nghiệm hình vuông Latin

Giá trị bị mất (y’) được tính bằng công thức:

(3.2.6.-2)

Trong đó, B’ và C’ là tổng các đáp ứng trong hàng và cột chứa giá trị bị mất. Trong bố trí thí nghiệm hình vuông Latin k = n. Giả sử giá trị 161 của đáp ứng ở cột thứ 1 và hàng thứ 1 trong Bảng 3.2.8.3.-II, ví dụ 3.2.8.3 bị mất, nó sẽ được thay thế bởi giá trị 150 tính được bằng công thức 3.2.6.-2 với:

B’ = 890

C’ = 876

T’ = 791

G’ = 6.175

k = 6

Các bậc tự do sẽ bị giảm xuống còn 19 đối với sai số dư và 34 đối với sai số toàn phần.

Bố trí thí nghiệm chéo

Nếu có giá trị bị mất trong kiểu bố trí thí nghiệm chéo phải tham khảo các tài liệu thống kê vì công thức tính sẽ rất khác nhau tùy theo cách phối hợp các xử lý.

3.2.7. Các định lượng đối xứng một phần

Nếu hoạt lực giả định của chế phẩm cần định lượng, là hoạt lực được dùng để tính lượng chế phẩm thử cần lấy khi pha các dung dịch thử của chế phẩm thử, khác xa với hoạt lực thật, nồng độ cao nhất hoặc nồng độ thấp nhất của chế phẩm thử có thể nằm lọt ra ngoài vùng tuyến tính của đường ln(liều) – đáp ứng, do đó định lượng sẽ không có giá trị thống kê do không thỏa mãn tính tuyến tính và/hoặc tính song song.

Có thể tính hoạt lực từ các số liệu còn lại, sau khi loại bỏ các đáp ứng của nồng độ cao nhất hoặc nồng độ thấp nhất của chế phẩm thử và dùng hoạt lực tính được để giả định lại hoạt lực của chế phẩm thử cho sát với hoạt lực thật hơn trong lần định lượng kế tiếp.

Logarithm tỷ lệ hoạt lực được tính bằng công thức:

(3.2.7.-1)

Công thức trên rất giống với phương trình 3.2.5.-3, tuy nhiên, ln(tỷ lệ hoạt lực) sẽ bị trừ đi một đại lượng bằng I/2 nếu bỏ nồng độ thấp nhất, và cộng thêm I/2 nếu bỏ nồng độ cao nhất.

Tính các đáp ứng trung bìnhvàtheo cách tương tự như định lượng cân xứng hoàn toàn (phương trình 3.2.5.-1), nhưng công thức tính độ dốc (b) có một số biến đổi tùy theo bố trí thí nghiệm.

Trong định lượng nhiều chế phẩm, mỗi chế phẩm có 2 liều, tính độ dốc bằng công thức:

(3.2.7.-2)

Chú ý: trong công thức trên, tử số không bao gồm L_U vì chế phẩm U chỉ còn một nồng độ.

Đối với định lượng chỉ có một chế phẩm thử:

(3.2.7.-3)

Trong định lượng đa chế phẩm, mỗi chế phẩm có 3 liều, tính các tương phản tuyến tính (L_S, …, L_Z) theo công thức cho ở Bảng 3.2.3.-II, riêng L_U tính bằng công thức ở Bảng 3.2.3.-I. Công thức tính độ dốc sẽ là:

(3.2.7.-4)

Đối với định lượng chỉ có một chế phẩm thử, công thức trên trở thành:

(3.2.7.-5)

3.2.8. Các ví dụ

Mục này trình bày một số ví dụ minh họa cách sử dụng các công thức tính toán liên quan đến mô hình đường thẳng song song.

Các ví dụ giới thiệu ở đây chỉ nhằm mục đích minh họa cho các phương pháp tính toán thống kê và không phải là phương pháp bắt buộc phải áp dụng nếu chuyên luận riêng cho phép dùng phương pháp khác.

Để có thể sử dụng các ví dụ trong chuyên luận này như nguồn số liệu chuẩn phục vụ cho việc kiểm tra các chương trình vi tính, thương mại hay tự biên soạn, dùng trong phân tích thống kê kết quả định lượng sinh học, các kết quả tính toán có thể chứa nhiều số thập phân hơn mức cần thiết. Có thể dùng phương pháp tính toán khác với phương pháp giới thiệu trong chuyên luận này, nhưng kết quả cuối cùng phải giống như các kết quả trong các ví dụ trình bày ở đây.

Ví dụ 3.2.8.1. Định lượng đồng thời nhiều chế phẩm thử, mỗi chế phẩm có 2 liều với bố trí thí nghiệm ngẫu nhiên hoàn toàn

Định lượng corticotrophin bằng phương pháp tiêm dưới da chuột

Liều chỉ định của chế phẩm chuẩn là 0,25 và 1,0 đơn vị cho mỗi 100 g thể trọng chuột thí nghiệm. Hai chế phẩm thử đều có hoạt lực giả định là 1 đơn vị/mg và có liều chỉ định giống như chế phẩm chuẩn. Các đáp ứng riêng và đáp ứng trung bình của mỗi nhóm xử lý cho ở Bảng 3.2.8.1.-I.

Bảng 3.2.8.1.-I - Đáp ứng metameter y - khối lượng Acid ascorbic (mg) trên 100 g tuyến thượng thận

	Chế phẩm chuẩn S		Chế phẩm thử U		Chế phẩm thử Z		Tổng số
	s₁	s₂	u₁	u₂	z₁	z₂	Tổng số
	300	289	310	230	250	236
	310	221	290	210	268	213
	330	267	360	280	273	283
	290	236	341	261	240	269
	364	250	321	241	307	251
	328	231	370	290	270	294
	390	229	303	223	317	223
	360	269	334	254	312	250
	342	233	295	216	320	216
	306	259	315	235	265	265
Trung bình	332,0	248,4	323,9	244,0	282,2	250,0
Phương sai (var_i)	1.026,7	483,8	725,0	718,7	854,6	784,7
ln (var_i)	6,9341	6,1817	6,5862	6,5774	6,7507	6,6653

Bảng 3.2.8.1.-II – Các tổng đáp ứng và tương phản tuyến tính (xem công thức tính ở Bảng 3.2.3.-I)

	Chế phẩm chuẩn S	Chế phẩm thử U	Chế phẩm thử Z	Tổng số
Liều thấp	S₁ = 3.320	U₁ = 3.239	Z₁ = 2.822
Liều cao	S₂ = 2.484	U₂ = 2.440	Z₂ = 2.500
Tổng đáp ứng của chế phẩm	S = 5.804	U = 5.679	Z = 5.322
Tương phản tuyến tính	L_S = -836	L_U = -799	L_S = -322

Tính các tổng các bình phương theo công thức trong các Bảng 3.2.3.-IV và 3.2.3.-V dùng các số liệu tính được ở Bảng 3.3.8.1.-IV:

Chế phẩm

Hồi qui tuyến tính =

Không song song =

Giữa các xử lý =

Toàn phần =

Sai số dư = Toàn phần – Giữa các xử lý = 119.646,58 – 78.305,68 = 41.340,90

Bảng 3.2.8.1.-III – Phân tích phương sai

Nguồn gây sai số	Bậc tự do	Tổng các bình phương	Bình phương trung bình	Tỷ số F	Xác suất
Chế phẩm	2	6.256,6	3128,3
Hồi qui tuyến tính	1	63.830,8	63.830,8	83,4	< 0,01
Không song song	2	8.218,2	4109,1	5,4	< 0,05
Giữa các xử lý	5	78.305,7
Sai số dư	54	41.340,9	765,6
Sai số toàn phần	59	119.646,6

Kiểm tra tính có giá trị của định lượng

Kết quả phân tích phương sai cho thấy, tỷ số F của biến số hồi qui F_cal = 83,4 rất lớn so với F tới hạn ở xác suất P = 0,01, f₁ = 1 và f₂ = 54: F_{(P = 0,01;f1 = 1;f2 = 54)} = 7,13[1], do đó biến số hồi qui rất có ý nghĩa.

Biến số không song song cũng có ý nghĩa, F_cal. = 5,4 > F_{(P = 0,05,f1 = 2,f2 = 54)}= 3,17. Khảo sát Bảng 3.2.8.1.-IV cho thấy chế phẩm Z có tương phản tuyến tính L_Z rất khác với L_S và L_U. Do đó, có khả năng độ dốc của đường ln(liều) – đáp ứng của chế phẩm Z không phù hợp với các chế phẩm còn lại và là nguyên nhân làm cho định lượng không có giá trị. Kiểm tra giả thuyết trên bằng phép kiểm tra Dunnett:

Đối với chế phẩm U:

Đối với chế phẩm Z:

Đối với chế phẩm Z,> t’ = 2,27 đọc từ Bảng 3.2.4.-II với P = 0,05, f₁ = 2 và f₂ = 54, do đó đường ln(liều) – đáp ứng của nó không song song với đường ln(liều) – đáp ứng của chế phẩm chuẩn. Loại các số liệu liên quan đến chế phẩm Z và lặp lại phân tích chỉ với chế phẩm U và chế phẩm chuẩn, với và .

Bảng 3.2.8.1.-IV – Phân tích phương sai không có chế phẩm Z

Nguồn gây sai số	Bậc tự do	Tổng các bình phương	Bình phương trung bình	Tỷ số F	Xác suất
Chế phẩm	1	390,6	390,6
Hồi qui tuyến tính	1	66.830,6	66.830,6	90,5	< 0,01
Không song song	1	34,2	34,2	0,05	> 0,05
Giữa các xử lý	3	67.255,5
Sai số dư	36	26.587,3	738,54
Sai số toàn phần	39	93.842,8

Sau khi loại chế phẩm Z, kết quả phân tích phương sai cho thấy định lượng có giá trị thống kê.

Tính hoạt lực và các giới hạn tin cậy

Tỷ lệ giữa các liều kế tiếp nhau bằng 1,0/0,25 = 4, do đó I = ln(4) = 1,3863, t = 2,03 với P = 0,95 và f = 36 (Bảng 5.1).

Hoạt lực giả định A_U của chế phẩm U là 1 đơn vị/mg, do đó:

Hoạt lực của chế phẩm U bằng antiln (M_U) = antiln (0,1060) = 1,11 đơn vị/mg.

Logarithm các giới hạn tin cậy bằng:

Các giới hạn tin cậy là 0,82 và 1,51 đơn vị/mg.

Ví dụ 3.2.8.2. Định lượng 3 liều với một chế phẩm thử, bố trí thí nghiệm ngẫu nhiên theo khối không lặp

Định lượng kháng sinh bằng phương pháp khuếch tán dùng hộp Petri

Các dung dịch thử của chế phẩm chuẩn s₁, s₂ và s₃ có nồng độ lần lượt là 2, 4 và 8 IU/ml. Chế phẩm thử có hoạt lực giả định là 1.500 IU/ml và cũng được pha thành 3 dung dịch thử u₁, u₂ và u₃ có nồng độ tương đương với nồng độ các dung dịch thử của chế phẩm chuẩn. Mỗi hộp Petri đều có 3 dung dịch thử của chế phẩm chuẩn và 3 dung dịch thử của chế phẩm thử, trong đó mỗi dung dịch thử chỉ xuất hiện một lần duy nhất (không lặp). Trật tự sắp xếp các dung dịch thử trong mỗi hộp hoàn toàn ngẫu nhiên và không giống nhau giữa các hộp (xem Bảng 3.2.8.2.-I).

Các đáp ứng riêng và đáp ứng trung bình của mỗi dung dịch thử cho ở Bảng 3.2.8.2.-II.

Bảng 3.2.8.2.-I – Cách bố trí các dung dịch thử

Hộp số	Trật tự sắp xếp các nồng độ của S và U trong mỗi hộp Petri
1	u₂	u₃	s₃	s₁	u₁	s₂
2	s₃	u₁	s₂	u₃	s₁	u₂
3	u₃	u₂	s₁	s₃	s₂	u₁
4	s₁	s₂	u₃	u₁	u₂	s₃
5	u₁	s₁	u₂	s₂	s₃	u₃
6	s₂	s₃	u₁	u₂	u₃	s₁

Bảng 3.2.8.2.-II - Đáp ứng y – đường kính vòng vô khuẩn ()

Hộp số	Chế phẩm chuẩn S			Chế phẩm thử U			Tổng khối
Hộp số	s₁	s₂	s₃	u₁	u₂	u₃	Tổng khối
1	176	205	235	174	202	232	R₁ = 1224
2	178	208	238	175	206	234	R₂ = 1239
3	178	207	237	177	203	236	R₃ = 1238
4	175	205	235	173	201	232	R₄ = 1221
5	176	206	235	174	204	231	R₅ = 1226
6	174	204	236	170	202	229	R₆ = 1215
Trung bình	176,2	205,8	236,0	173,8	203,0	232,3
Phương sai	2,6	2,2	1,6	5,4	3,2	5,9

Kiểm tra số liệu thu được bằng các phép kiểm tra tương tự như ở ví dụ 3.2.8.1 cho thấy định lượng đáp ứng các điều kiện ở mục 3.1.1.

Bảng 3.2.8.2.-III – Các tổng đáp ứng và tương phản tuyến tính (xem công thức tính ở Bảng 3.2.3.-II)

	Chế phẩm chuẩn S	Chế phẩm thử U	Tổng số
Liều thấp	S₁ = 1.075	U₁ = 1.043
Liều trung bình	S₂ = 1.235	U₂ = 1.218
Liều cao	S₃ = 1.416	U₃ = 1.394
Tổng đáp ứng của chế phẩm	S = 3.708	U = 3.655
Tương phản tuyến tính	L_S = 359	L_U = 351
Tương phản bậc hai	Q_S = 3	Q_U = 1

Các tổng các bình phương được tính bằng các công thức trong Bảng 3.2.3.-IV và 3.2.3.-V với các giá trị ở Bảng 3.2.8.2.-III.

Chế phẩm

Hồi qui tuyến tính =

Không song song =

Độ cong =

Giữa các xử lý =

Giữa các khối =

Toàn phần =

Sai số dư = Toàn phần – Giữa các xử lý – Giữa các khối = 28,03

Bảng 3.2.8.2.-IV – Phân tích phương sai

Nguồn gây sai số	Bậc tự do	Tổng các bình phương	Bình phương trung bình	Tỷ số F	Xác suất
Chế phẩm	1	78,03	78,03
Hồi qui tuyến tính	1	21.004,17	21.004,17	18.737	< 0,01
Không song song	1	2,67	2,67	2,4	> 0,05
Độ cong	2	0,28	0,16	0,1	> 0,05
Giữa các xử lý	5	21.085,14
Giữa các khối (hộp Petri)	5	75,80	15,16	13,5	< 0,01
Sai số dư	25	28,03	1,121
Sai số toàn phần	35	21.188,97

Kết quả phân tích phương sai cho thấy sự khác nhau có ý nghĩa (P < 0,01) của kích thước đường kính vòng vô khuẩn giữa các hộp Petri. Nếu thí nghiệm bố trí theo kiểu ngẫu nhiên hoàn toàn, sai số giữa các khối sẽ không được tách ra khỏi sai số toàn phần, do đó sai số dư s² sẽ lớn hơn, dẫn đến khoảng tin cậy sẽ rộng hơn. Đây là ưu điểm của bố trí thí nghiệm ngẫu nhiên theo khối so với bố trí thí nghiệm kiểu ngẫu nhiên hoàn toàn.

Kiểm tra giá trị của định lượng

Hồi qui tuyến tính rất có ý nghĩa (P < 0,01), các đại lượng không song song và độ cong không có ý nghĩa (P > 0,05), do đó định lượng có giá trị thống kê.

Tính hoạt lực và các giới hạn tin cậy

Tỷ lệ giữa các nồng độ kế tiếp bằng 2,0, do đó:

Với P = 0,95 và f = 25, t = 2,06 (Bảng 5.1).

Hoạt lực của chế phẩm U là R = antiln(M) = 1.400 IU/ml.

Các ln(giới hạn tin cậy) bằng:

Các giới hạn tin cậy bằng 1.378 và 1.423 IU/ml.

Nếu phân tích bằng máy tính, các kết quả sẽ là:

Khoảng tin cậy: 1.376,3 – 1.424,1 IU/ml.

Ví dụ 3.2.8.3. Định lượng 3 liều với một chế phẩm thử, bố trí thí nghiệm theo hình vuông Latin không lặp

Định lượng kháng sinh bằng phương pháp khuếch tán, dùng khay vuông

Chế phẩm chuẩn có hoạt lực biết trước 4.855 IU/mg. Chế phẩm thử có hoạt lực giả định là 5.600 IU/mg. Pha các dung dịch gốc bằng cách hòa tan 25,2 mg chế phẩm chuẩn và 21,4 mg chế phẩm thử trong lượng vừa đủ dung môi pha loãng để được 25 ml. Sau đó, pha loãng các dung gốc đến nồng độ pha loãng 1/20 và tiếp tục pha loãng xa hơn với tỷ lệ pha loãng 1:1,5 để được các dung dịch thử cuối cùng của chuẩn và mẫu.

Các dung dịch thử của chuẩn và mẫu được bố trí trên khay theo bố trí thí nghiệm hình vuông Latin như trong Bảng 3.2.8.3.-I. Các đường kính vòng vô khuẩn của định lượng trình bày trong Bảng 3.2.8.3.-II. Trung bình đường kính vòng vô khuẩn, phương sai (var_i) và ln(var_i) của mỗi nhóm dung dịch thử trình bày trong Bảng 3.2.8.3.-III.

Bảng 3.2.8.3.-I. Cách bố trí các dung dịch thử trên khay

	1	2	3	4	5	6
1	s₁	u₁	u₂	s₃	s₂	u₃
2	u₁	u₃	s₁	s₂	u₂	s₃
3	u₂	s₃	s₂	s₁	u₃	u₁
4	s₃	s₂	u₃	u₁	s₁	u₂
5	s₂	u₂	s₃	u₃	u₁	s₁
6	u₃	s₁	u₁	u₂	s₃	s₂

Kiểm tra tính đồng nhất của các phương sai

Đối với một nhóm gồm k phương sai, trong đó mỗi phương sai có f = ( n – 1) bậc tự do, công thức tính sẽ như sau:

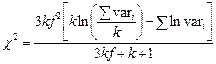
Với k = 6, bậc tự do f = 5, công thức trên sẽ rút gọn thành:

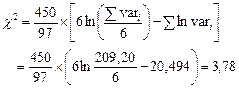
Giá trị tính được nhỏ hơn giá trị tới hạn 11,07 đọc từ Bảng 5.2 với P = 0,95 và f = (k – 1) = 5. Do đó, sự khác biệt giữa các phương sai của mỗi nhóm dung dịch thử không có ý nghĩa thống kê.

Bảng 3.2.8.3.-II Đáp ứng y – đường kính vòng vô khuẩn ()

	1	2	3	4	5	6	Tổng hàng
1	161	160	178	187	171	194	R₁ = 1.051
2	151	192	150	172	170	192	R₂ = 1.027
3	162	195	174	161	193	151	R₃ = 1.036
4	194	184	199	160	163	171	R₄ = 1.071
5	176	181	201	202	154	151	R₅ = 1.065
6	193	166	161	186	198	182	R₆ = 1.086
Tổng cột	C₁ = 1.037	C₂ = 1.078	C₃ = 1.063	C₄ = 1.068	C₅ = 1.049	C₆ = 1.041

Bảng 3.2.8.3.-III Trung bình đường kính vòng vô khuẩn và phương sai của mỗi nhóm dung dịch thử

	Chế phẩm chuẩn S			Chế phẩm thử U			Tổng số
	s₁	s₂	s₃	u₁	u₂	u₃	Tổng số
	161	171	187	160	178	194
	150	172	192	151	170	192
	161	174	195	151	162	193
	163	184	194	160	171	199
	151	176	201	154	181	202
	166	182	198	161	186	193
Trung bình	158,67	176,50	194,50	156,17	174,67	195,50
Phương sai (var_i)	43,47	28,70	23,50	22,17	75,07	16,30
ln (var_i)	3,772	3,357	3,157	3,099	4,318	2,791

Bảng 3.2.8.3.-IV – Các tổng đáp ứng và tương phản tuyến tính (xem công thức tính ở Bảng 3.2.3.-II)

	Chế phẩm chuẩn S	Chế phẩm thử U	Tổng số
Liều thấp	S₁ = 952	U₁ = 937
Liều trung bình	S₂ = 1.059	U₂ = 1.048
Liều cao	S₃ = 1.167	U₃ = 1.173
Tổng đáp ứng của chế phẩm	S = 3.178	U = 3.158
Tương phản tuyến tính	L_S = 215	L_U = 236
Tương phản bậc hai	Q_S = 1	Q_U = 14

Các tổng các bình phương được tính bằng các công thức trong Bảng 3.2.3.-IV và 3.2.3.-V với các giá trị ở Bảng 3.2.8.3.-II và Bảng 3.2.8.3.-IV.

Chế phẩm

Hồi qui tuyến tính =

Không song song =

Độ cong (không tuyến tính) =

Giữa các xử lý =

Giữa các hàng =

Giữa các cột =

Toàn phần =

Sai số dư = Toàn phần – Giữa các xử lý – Giữa các hàng – Giữa các cột = 415,3333

Bảng 3.2.8.3.-V – Phân tích phương sai

Nguồn gây sai số	Bậc tự do	Tổng các bình phương	Bình phương trung bình	Tỷ số F	Xác suất
Chế phẩm	1	11,1111	11,1111
Hồi qui tuyến tính	1	8.475,0417	8.475,0417	408,1	< 0,01
Không song song	1	18,3750	18,3750	0,885	> 0,05
Độ cong	2	5,4722	2,7361	0,132	> 0,05
Giữa các xử lý	5	8510
Giữa các hàng	5	412	82,40	3.968	< 0,05
Giữa các cột	5	218,6667	43,73	2,106	> 0,05
Sai số dư	20	415,3333	20,7667
Sai số toàn phần	35	9.556

Phân tích phương sai cho thấy sự khác nhau có ý nghĩa (P < 0,05) giữa các hàng chứng tỏ bố trí thí nghiệm hình vuông Latin cho độ chính xác cao hơn bố trí thí nghiệm ngẫu nhiên hoàn toàn.

Kiểm tra tính có giá trị của định lượng

Hồi qui tuyến tính rất có ý nghĩa (P < 0,01), độ lệch khỏi tính tuyến tính và tính song song của các đường ln(liều) – đáp ứng không có ý nghĩa (P > 0,05), do đó định lượng thỏa mãn các phép kiểm tra tính có giá trị.

Tính hoạt lực và các giới hạn tin cậy

Tỷ lệ giữa các nồng độ kế tiếp nhau bằng 1,5, do đó I = ln(1,5) = 0,405465. Với P = 0,95 và f = 20, t = 2,09 (Bảng 5.1).

Hoạt lực của chế phẩm U là R = antiln(M) = 5.467,3 IU/mg.

Các ln(giới hạn tin cậy) được tính theo công thức:

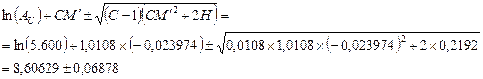
Các giới hạn tin cậy bằng 5.102,6 và 5.855,1 IU/mg.

Vì các dung dịch gốc của chế phẩm chuẩn và chế phẩm thử không hoàn toàn bằng nhau, cần hiệu chỉnh hoạt lực tính được và các giới hạn tin cậy bằng cách nhân với một hệ số hiệu chỉnh:

Sau khi hiệu chỉnh, hoạt lực tính được sẽ bằng 5.582 IU/mg với giới hạn tin cậy từ 5.209 đến 5.977 IU/mg ở xác suất 95 %.

Ví dụ 3.2.8.4. Định lượng chéo đôi

Định lượng insulin bằng phương pháp tiêm dưới da thỏ

Các dung dịch thử của chế phẩm chuẩn có nồng độ 1 và 2 IU/ml. Hoạt lực giả định của chế phẩm thử là 40 IU/ml và được pha loãng thành các dung dịch thử có nồng độ tương đương với các dung dịch thử của chế phẩm chuẩn. Tiêm dưới da các thỏ thí nghiệm với liều 0,5 ml mỗi dung dịch thử theo sơ đồ ở Bảng 3.2.8.4.-I. Các kết quả thí nghiệm trình bày trong Bảng 3.2.8.4.-II. Phương sai lớn cho thấy đáp ứng không đồng nhất của các thỏ thí nghiệm với hoạt chất cần định lượng và giải thích cho sự cần thiết phải dùng bố trí thí nghiệm chéo.

Bảng 3.2.8.4.-I – Cách sắp xếp các xử lý

Ngày thí nghiệm	Nhóm thỏ
Ngày thí nghiệm	1	2	3	4
Ngày I	s₁	s₂	u₁	u₂
Ngày II	u₂	u₁	s₂	s₁

Kiểm tra tính đồng nhất của các phương sai bằng phép kiểm tra Hartley

Tính tỷ số F theo công thức:

Trong đó var_max. là phương sai lớn nhất và var_min. là phương sai nhỏ nhất trong k phương sai cần kiểm tra. F tính được nhỏ hơn F tới hạn bằng 12,7 đọc từ Bảng 5.3 với P = 0,95, k = 8 và bậc tự do f = 7. Do đó, sự khác nhau giữa các phương sai của mỗi nhóm dung dịch thử không có ý nghĩa thống kê. Nếu dùng phép kiểm tra Bartlett với cùng số liệu, giá trị tính được sẽ là 6,4 so với giá trị tới hạn bằng 14,1.

Trong các định lượng bố trí thí nghiệm chéo, các tổng đáp ứng và tương phản tuyến tính được tính riêng rẽ cho mỗi giai đoạn thí nghiệm. Kết quả tính toán trình bày trong Bảng 3.2.8.4.-III.

Bảng 3.2.8.4.-II – Đáp ứng y: glucose huyết (mg/100 ml) ở 1 và 1½ giờ

	Nhóm 1			Nhóm 2			Nhóm 3			Nhóm 4
	s₁	u₂	Tổng số	s₂	u₁	Tổng số	u₁	s₂	Tổng số	u₂	s₁	Tổng số
	112	104	216	65	72	137	105	91	196	118	144	262
	126	112	238	116	160	276	83	67	150	119	149	268
	62	58	120	73	72	145	125	67	192	42	51	93
	86	63	149	47	93	140	56	45	101	64	107	171
	52	53	105	88	113	201	92	84	176	93	117	210
	110	113	223	63	71	134	101	56	157	73	128	201
	116	91	207	50	65	115	66	55	121	39	87	126
	101	68	169	55	100	155	91	68	159	31	71	102
Trung bình	95,6	82,8		69,6	93,3		89,9	66,6		72,4	106,8
Phương sai	709,7	627,9		525,1	1.012,5		479,6	230,6		1.214,3	1.215,1

Bảng 3.2.8.4.-III – Các tổng đáp ứng và tương phản tuyến tính

	Chế phẩm chuẩn S	Chế phẩm thử U	Tổng số
Ngày I
Nồng độ thấp	S_1I = 765	U_1I = 719
Nồng độ cao	S_2I = 557	U_2I = 579
Tổng số	S_I = 1.322	U_I = 1.298	D_I = 2.620

Ngày II
Nồng độ thấp	S_1II = 854	U_1II = 746
Nồng độ cao	S_2II = 533	U_2II = 662
Tổng số	S_II = 1.387	U_II = 1.408	D_II = 2.795

Tổng chế phẩm	S = 2.709	U = 2.706

Tương phản tuyến tính
Ngày I	L_SI = -208	L_UI = -140	L_I = -348
Ngày II	L_SII = -321	L_UII = -84	L_II = -405
Tổng số	L_S = -529	L_U = -224

Phân tích phương sai trong các định lượng bố trí thí nghiệm chéo phức tạp hơn các kiểu bố trí thí nghiệm khác do độ phân tán, biểu diễn bằng tổng các bình phương, gây bởi tính song song không độc lập với độ phân tán giữa các đơn vị thí nghiệm (trong ví dụ này là thỏ). Tính song song của các đường hồi qui sẽ được kiểm tra bằng một đại lượng sai số bình phương trung bình phụ, được tính bằng cách lấy tổng các bình phương giữa các thỏ thí nghiệm trừ đi thành phần song song và hai thành phần tương tác.

Ba thành phần tương tác được đưa thêm vào phân tích phương sai gây bởi sự lặp lại trong mỗi nhóm thỏ thí nghiệm, gồm:

giữa các ngày chế phẩm; giữa các ngày hồi qui; giữa các ngày tính song song.

Ba đại lượng này biểu thị khuynh hướng biến thiên từ ngày thí nghiệm này sang ngày thí nghiệm khác của các nguồn gây sai số do chế phẩm, hồi qui và tính song song. Giá trị thống kê của định lượng phụ thuộc vào mức ý nghĩa của các tỷ số F tương ứng của ba đại lượng nói trên. Nếu F tính được rất có ý nghĩa, F_cal. > F_crit.ở P = 0,01, cần phải rất thận trọng khi suy diễn các kết quả của định lượng, nếu có thể, phải lặp lại định lượng.

Tính giá trị của tổng các bình phương của chế phẩm, hồi qui và không song song theo công thức trong Bảng 3.2.3.-IV với số liệu trong Bảng 3.2.8.4.-III.

Chú ý trong định lượng này n = 16, là tổng số đáp ứng của mỗi xử lý qua hai ngày thí nghiệm.

Chế phẩm

Hồi qui tuyến tính =

Không song song =

Giữa các khối (thỏ) =

trong đó B_i là các tổng đáp ứng của mỗi thỏ thí nghiệm trong Bảng 3.2.8.4.-II.

Giữa các ngày =

trong đó D_I và D_II là tổng đáp ứng của mỗi ngày thí nghiệm.

Giữa các ngày Chế phẩm =

trong đó S_I, S_II, U_I và U_II là tổng đáp ứng của từng chế phẩm trong mỗi ngày.

Giữa các ngày hồi qui =

Giữa các ngày Không song song =

trong đó L_SI, L_SII, L_UI và L_UII là tương phản tuyến tính của mỗi ngày thí nghiệm.

Toàn phần =

Sai số dư giữa các thỏ = Giữa các khối – Không song song – (giữa các ngày chế phẩm) – (giữa các ngày hồi qui) = 39.794,73 – 1.453,51 – 31,64 – 50,76 = 38.258,81

Sai số dư trong mỗi thỏ = Toàn phần – Giữa các khối – Giữa các ngày – Chế phẩm – Hồi qui – (giữa các ngày không song song) = 53.423,23 – 39.794,73 – 478,51 – 0,14 – 8.859,52 – 446,27 = 3.844,06

Tính có giá trị của định lượng

Phân tích phương sai cho thấy định lượng thỏa mãn phép kiểm tra tính có giá trị:

1) Hồi qui tuyến tính rất có ý nghĩa: tỷ số F của đại lượng hồi qui được tính dựa trên sai số bình phương trung bình trong mỗi thỏ, F_cal. = 64,5 > F_crit. = 7,63 với P = 0,01, f₁ = 1 và f₂ = 28.

2) Tính song song của đường hồi qui: phép kiểm tra tính song song trong định lượng chéo dựa trên sai số bình phương trung bình giữa các thỏ, F_cal. = 1,06 < F(_P_{= 0,05, f1 = 1, f2 = 28}) = 4,19, chứng tỏ các đường ln(liều) – đáp ứng của chuẩn và mẫu song song với nhau.

3) Ba thành phần tương tác đều không có ý nghĩa, các tỷ số F tính được lần lượt là 0,02, 0,04 và 3,25 và đều nhỏ hơn F_crit. = 4,19.

Bảng 3.2.8.4.-IV – Phân tích phương sai

Nguồn gây sai số	Bậc tự do	Tổng các bình phương	Bình phương trung bình	Tỷ số F	Xác suất
Không song song	1	1.453,5	1.453,5	1,06	> 0,05
Giữa các ngày chế phẩm	1	31,6	31,6	0,02	> 0,05
Giữa các ngày hồi qui	1	50,8	50,8	0,04	> 0,05
Sai số dư giữa các thỏ	28	38.258,8	1.366,4
Giữa các khối (thỏ)	31	39.794,7	1.283,7
Chế phẩm	1	0,1	0,1	0,00	> 0,05
Hồi qui	1	8.859,5	8.859,5	64,5	< 0,01
Giữa các ngày	1	478,5	478,5	3,48	> 0,05
Giữa các ngày không song song	1	446,3	446,3	3,25	> 0,05
Sai số dư trong mỗi thỏ	28	3.844,1	137,3
Toàn phần	63	53.423,2	847,9878472

Tính hoạt lực và các giới hạn tin cậy

Tỷ lệ pha loãng bằng 2, do đó I = ln(2) = 0,69315. Với P = 0,95 và f = 28, t = 2,05 (Bảng 5.1).

Hoạt lực R = antiln(M) = antiln(0,00276) = 40,1 IU/ml.

Logarithm các giới hạn tin cậy bằng:

Giới hạn tin cậy của hoạt lực từ 33,4 đến 48,2 IU/ml.

4. Phối hợp các kết quả định lượng

4.1. Mở đầu

Để đáp ứng các yêu cầu của Dược điển, ví dụ yêu cầu về độ chính xác, có thể phải lặp lại hai hay nhiều định lượng độc lập và phối hợp các kết quả định lượng để được kết quả cuối cùng chính xác và đáng tin cậy hơn.

Hai định lượng được coi là độc lập với nhau nếu quá trình thực hiện của mỗi định lượng không gây bất cứ ảnh hưởng nào đến kết quả của định lượng khác. Điều đó có nghĩa là các sai số ngẫu nhiên của các yếu tố chủ yếu có thể ảnh hưởng đến kết quả định lượng (ví dụ: sự chuẩn bị các dung dịch thử của chuẩn và mẫu thử, độ nhạy của chỉ thị sinh học) của một định lượng phải độc lập với các sai số ngẫu nhiên tương ứng của định lượng kia. Các định lượng thực hiện vào những ngày kế tiếp nhau dùng cùng dung dịch gốc của chế phẩm chuẩn không phải là những định lượng độc lập.

Có nhiều phương pháp phối hợp kết quả của các định lượng độc lập, tuy nhiên, dưới đây chỉ trình bày ba phương pháp gần đúng do tính đơn giản và dễ áp dụng của chúng.

Trước khi phối hợp, các hoạt lực phải được hiệu chỉnh với hoạt lực giả định của mỗi chế phẩm thử (xem ví dụ 3.2.8.3) và phải được biểu diễn dưới dạng logarithm.

4.2. Phối hợp cân chỉnh các kết quả định lượng (weighted combination)

Phương pháp này có thể áp dụng nếu thỏa mãn các điều kiện sau:

1) các định lượng phải độc lập với nhau;

2) đại lượng C của mỗi định lượng phải nhỏ hơn 1,1 (xem công thức 3.2.5-6 để biết công thức tính và ý nghĩa của C);

3) bậc tự do của sai số dư của mỗi định lượng phải lớn hơn 6, tốt nhất là lớn hơn 15;

4) sự khác nhau giữa các hoạt lực cần phối hợp phải không có ý nghĩa thống kê (xem mục 4.2.2).

Nếu các điều kiện trên không thỏa mãn, dùng phương pháp giới thiệu ở mục 4.3 để tính hoạt lực trung bình và lấy kết quả tính được làm hoạt lực giả định cho lần định lượng kế tiếp.

4.2.1. Tính các hệ số cân chỉnh W

Giả sử các kết quả đo của mỗi n’ định lượng đã được phân tích để được n’ giá trị logarithm hoạt lực M và các giới hạn tin cậy tương ứng. Đối với mỗi định lượng, tính logarithm khoảng giới hạn tin cậy L bằng cách lấy logarithm giới hạn tin cậy trên trừ đi logarithm giới hạn tin cậy dưới. Tính hệ số W cho mỗi giá trị M theo phương trình 4.2.1.-1, với t là số Student đã dùng khi tính các giới hạn tin cậy.

(4.2.1.-1)

4.2.2. Tính đồng nhất của các hoạt lực

Để kiểm tra tính đồng nhất của một dãy các hoạt lực, thành lập biểu thức có phân phối xấp xỉ phân phối như sau:

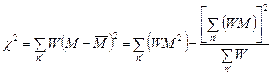(4.2.2.-1)

với:

Nếu tính được nhỏ hơn giá trị tương ứng với bậc tự do f = (n’ – 1) tra từ Bảng 5.2, sự khác nhau giữa các hoạt lực không có ý nghĩa thống kê và, do đó, có thể tiếp tục tính hoạt lực trung bình và các giới hạn tin cậy theo các công thức ở mục 4.2.3.

Nếu tính được lớn hơn giá trị tới hạn tương ứng đọc từ Bảng 5.2, các hoạt lực tính được không đồng nhất và không thể sử dụng các công thức ở mục 4.2.3, thay vào đó, có thể dùng các công thức ở mục 4.2.4.

4.2.3. Tính hoạt lực trung bình có cân chỉnh (weighted mean) và các giới hạn tin cậy

Logarithm hoạt lực trung bình được tính theo công thức:

(4.2.3.-1)

Độ lệch chuẩn của logarithm hoạt lực trung bình là căn bậc hai của nghịch đảo của tổng các hệ số W:

(4.2.3.-2)

và các logarithm giới hạn tin cậy của hoạt lực trung bình được tính theo phương trình sau:

(4.2.3.-3)

trong đó t là số Student đọc từ Bảng 5.2 với bậc tự do bằng tổng số bậc tự do của các sai số dư của mỗi định lượng.

4.2.4. Hoạt lực trung bình có cân chỉnh và các giới hạn tin cậy dựa trên độ phân tán trong mỗi định lượng và giữa các định lượng

Khi phối hợp các kết quả của một số định lượng lặp lại, giá trị có thể có ý nghĩa. Độ phân tán của các hoạt lực có thể phân tích thành hai thành phần, gồm:

1) Phương sai trong mỗi định lượng

2) Phương sai giữa các định lượng

với là trung bình chưa cân chỉnh (trung bình số học) của các M. Phương sai đầu thay đổi từ định lượng này đến định lượng khác, trong khi phương sai sau là chung cho tất cả các M.

Đối với mỗi M tính hệ số cân chỉnh theo công thức:

Dùng W’ thay thế cho W trong các công thức ở mục 4.2.3, với t = 2.

4.3. Phối hợp không cân chỉnh các kết quả định lượng (unweighted combination)

Phương pháp phối hợp các kết quả định lượng đơn giản nhất là tính trung bình số học của n’ logarithm hoạt lực M và sau đó tính độ lệch chuẩn của nó theo công thức:

(4.3.-1)

các logarithm giới hạn tin cậy bằng:

(4.3.-2)

trong đó t có (n’ – 1) bậc tự do. Vì số các định lượng cần phối hợp thường nhỏ nên giá trị của t khá lớn.

4.4. Ví dụ

Bảng 4.4.-1 liệt kê kết quả sáu định lượng độc lập cùng với các giới hạn tin cậy và bậc tự do của sai số dư tương ứng. Tất cả các định lượng đều đáp ứng điều kiện 1, 2 và 3 trong mục 4.2. Các hệ số W được tính theo công thức ở mục 4.2.

Kiểm tra tính đồng nhất của các hoạt lực

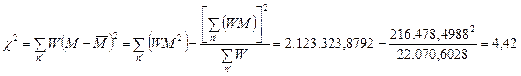
tính được nhỏ hơn giá trị tới hạn bằng 11,07 đọc từ Bảng 5.2 với bậc tự do f = 5. Do đó, sự khác nhau giữa các hoạt lực không có ý nghĩa thống kê.

Bảng 4.4.-I – Hoạt lực và các giới hạn tin cậy của sáu định lượng độc lập

Lần định lượng	Hoạt lực R (IU/lọ)	Các giới hạn tin cậy (IU/lọ)		Bậc tự do DF
Lần định lượng	Hoạt lực R (IU/lọ)	Giới hạn dưới	Giới hạn trên	Bậc tự do DF
1	18.367	17.755	19.002	20
2	18.003	17.415	18.610	20
3	18.064	17.319	18.838	20
4	17.832	17.253	18.429	20
5	18.635	17.959	19.339	20
6	18.269	17.722	18.834	20
Tổng số				120

Bảng 4.4.-II.

	M = ln(R)	L^*	W	MW	WM²
	9,8183	0,0679	3.777,8301	37.091,9101	364.179,9033
	9,7983	0,0664	3.951,6825	38.719,7456	379.387,4392
	9,8017	0,0841	2.462,5579	24.137,1950	236.584,9721
	9,7887	0,0659	4.003,1116	39.185,4586	383.576,6531
	9,8328	0,0740	3.175,7400	31.226,4061	307.042,9060
	9,8130	0,0609	4.699,6807	46.117,7833	452.552,0054
Tổng số	58,8528		22.070,6028	216.478,4988	2.123.323,8792

* L = ln(giới hạn tin cậy trên) – ln(giới hạn tin cậy dưới)

Hoạt lực trung bình và các giới hạn tin cậy

Hoạt lực trung bình và các giới hạn tin cậy của nó được tính bằng các công thức ở mục 4.2.3 và các số liệu trong Bảng 4.4.-I và 4.4.-II.

Với số bậc tự do f = 120, P = 0,95, t = 1,98.

Bằng cách lấy antilogarithm các giá trị tính được, hoạt lực trung bình bằng 18.187 IU/lọ với khoảng tin cậy ở xác suất 95 % từ 17.946 đến 18.431 IU/lọ.

5. Các Bảng tra cứu

5.1. Bảng mức ý nghĩa của t (giá trị tuyệt đối)

	P			P
f	0,95	0,99	f	0,95	0,99
1	12,71	63,66	18	2,10	2,88
2	4,30	9,92	19	2,09	2,86
3	3,18	5,84	20	2,09	2,85
4	2,78	4,60	21	2,08	2,83
5	2,57	4,03	22	2,07	2,82
6	2,45	3,71	23	2,07	2,81
7	2,36	3,50	24	2,06	2,80
8	2,31	3,36	25	2,06	2,79
9	2,26	3,25	26	2,06	2,78
10	2,23	3,17	27	2,05	2,77
11	2,20	3,11	28-29	2,05	2,76
12	2,18	3,05	30	2,04	2,75
13	2,16	3,01	40-43	2,02	2,7
14	2,14	2,98	57-63	2,00	2,66
15	2,13	2,95	102-126	1,98	2,26
16	2,12	2,92	600-∞	1,96	2,58
17	2,11	2,90
Nếu giá trị quan sát lớn hơn giá trị trong bảng, nó được coi là có ý nghĩa (P = 0,95) hay rất có ý nghĩa (P = 0,99).

5.2. Bảng mức ý nghĩa của

	P			P
f	0,05	0,01	f	0,05	0,01
1	3,84	6,63	11	19,68	24,73
2	5,99	9,21	12	21,03	26,22
3	7,81	11,34	13	22,36	27,69
4	9,49	13,28	14	23,68	29,14
5	11,07	15,09	15	25,00	30,58
6	12,59	16,81	16	26,30	32,00
7	14,07	18,48	20	31,41	37,57
8	15,51	20,09	25	37,65	44,31
9	16,92	21,67	30	43,77	50,89
10	18,31	23,21	40	55,76	63,69
Nếu giá trị quan sát lớn hơn giá trị trong bảng, nó được coi là có ý nghĩa (P = 0,95) hay rất có ý nghĩa (P = 0,99).

5.3. Mức ý nghĩa của tỷ số F = var_max/var_min của k phương sai trong nhóm xử lý, mỗi phương sai có f bậc tự do (Hartley’s test).

k
f	4	6	8	9	10	12
4	20,6	29,5	37,5	41,1	44,6	51,4
	49	69	89	97	106	120

5	13,7	18,7	22,9	24,7	26,5	29,9
	28	38	46	50	54	60

6	10,4	13,7	16,3	17,5	18,6	20,7
	19,1	25	30	32	34	37

7	8,44	10,8	12,7	13,5	14,3	15,8
	14,5	18,4	22	23	24	27

8	7,18	9,03	10,5	11,1	11,7	12,7
	11,7	14,5	16,9	17,9	18,9	21

9	6,31	7,80	8,95	9,45	9,91	10,7
	9.9	12,1	13,9	14,7	15,3	16,6

10	5,67	6,92	7,87	8,28	8,66	9,34
	8,6	10,4	11,8	12,4	12,9	13,9
Nếu F tính được lớn hơn giá trị trong bảng, biến số cần kiểm tra được coi là có ý nghĩa (dòng trên, P = 0,05), hay rất có ý nghĩa (dòng dưới, P = 0,01).

6. Các ký hiệu thuật ngữ

Ký hiệu	Định nghĩa
b	Độ dốc hồi qui tuyến tính của đường thẳng liều – đáp ứng hay ln(liều) – đáp ứng của tất cả các chế phẩm trong một định lượng
d	Số liều của mỗi chế phẩm trong một định lượng đối xứng.
e	cơ số của logarithm tự nhiên. e = 2,718281828….
f	số bậc tự do
h	số chế phẩm trong một định lượng, bao gồm cả chế phẩm chuẩn
k	số xử lý trong một định lượng, k = dh
n	số đáp ứng hay số lần lặp lại của mỗi xử lý
n’	số các ước lượng hoạt lực
s	độ lệch chuẩn,
s₁,s₂,s₃	Nồng độ thấp, trung bình và cao của chế phẩm S, trong một định lượng chỉ có 2 nồng độ của mỗi chế phẩm s₂ đại diện cho nồng độ cao
s²	ước lượng của sai số dư được tính từ sai số bình phương trung bình. là phương sai của logarithm hoạt lực M
t	thống kê Student (Bảng 5.1)
t’	thống kê Dunnett (Bảng 3.2.4.-II)
u₁…z₃	Nồng độ các dung dịch thử của chế phẩm cần định lượng U … Z
y	đáp ứng riêng hay đáp ứng riêng đã được biến đổi
y’	đáp ứng tính được dùng để thay thế cho giá trị bị mất
	đáp ứng trung bình của chế phẩm chuẩn và các chế phẩm thử
A_U…A_Z	hoạt lực giả định của các chế phẩm cần định lượng, là hoạt lực được dùng để tính lượng chế phẩm cần lấy khi pha các dung dịch thử
B₁…B_2n	tổng đáp ứng của mỗi đơn vị thí nghiệm (1 đến n) trong định lượng chéo đôi
B’	tổng đáp ứng của khối hay hàng có chứa giá trị bị mất
C	đại lượng biểu thị ý nghĩa của hồi qui, dùng trong tính toán các giới hạn tin cậy (phương trình 3.2.5-5). Trong một số tài liệu thống kê định lượng sinh học, ý nghĩa của hồi qui được biểu thị bằng g:
C₁…C_n	tổng đáp ứng của mỗi cột (1 đến n) trong bố trí thí nghiệm hình vuông Latin
C’	tổng đáp ứng của cột có chứa giá trị bị mất trong bố trí thí nghiệm hình vuông Latin
D	liều
D_I,D_II	tổng đáp ứng của giai đoạn I và giai đoạn II trong định lượng chéo đôi
E	tổng các bình phương của đại lượng hồi qui (Bảng 3.2.3.-IV)
F	tỷ số của hai ước lượng phương sai độc lập (Bảng 3.2.4.-I)
G’	tổng đáp ứng trong một định lượng có giá trị bị mất
I	khoảng cách giữa các ln(liều) kế tiếp nhau, ví dụ I = ln(S₂) – ln(S₁)
K	đại lượng được dùng để tính tổng các bình phương trong phân tích phương sai
L	độ rộng của logarithm giới hạn tin cậy, L = ln(giới hạn tin cậy trên) – ln(giới hạn tin cậy dưới)
L_S…L_Z	tương phản tuyến tính của chế phẩm chuẩn và các chế phẩm thử (Bảng 3.2.3.-I, 3.2.3.-II và 3.2.3.-III)
M	ước lượng của logarithm hoạt lực, trong định lượng đa chế phẩm M được dùng kèm với các ký tự U…Z , ví dụ M_U, để phân biệt giữa các chế phẩm
	trung bình của một vài M độc lập
M’	logarithm tỷ lệ hoạt lực hay ước lượng của hoạt lực trước khi hiệu chỉnh với hoạt lực giả định
N	tổng số đáp ứng trong một định lượng
N_S,N_U	tổng số đáp ứng của chế phẩm S và U
P	xác suất
Q_S…Q_Z	tương phản bậc hai của chế phẩm chuẩn và các chế phẩm thử
R	hoạt lực tính được – dùng với các ký tự đại diện cho chế phẩm thử để phân biệt giữa các chế phẩm trong một định lượng đa chế phẩm
R₁…R_n	tổng đáp ứng của mỗi hàng (1 đến n) trong bố trí thí nghiệm hình vuông Latin, hay mỗi khối trong bố trí thí nghiệm ngẫu nhiên theo khối
S	chế phẩm chuẩn
S	tổng đáp ứng của chế phẩm chuẩn
S₁,S₂,S₃	tổng đáp ứng của liều thấp, trung bình và cao của chế phẩm S, trong một định lượng chỉ có 2 nồng độ của mỗi chế phẩm S₂ đại diện cho nồng độ cao
T’	tổng đáp ứng trong một xử lý có giá trị bị mất
U…Z	tổng đáp ứng của các chế phẩm thử U…Z
U…Z	các chế phẩm cần định lượng
U₁,U₂,U₃	tổng đáp ứng của liều thấp, trung bình và cao của chế phẩm U, trong một định lượng chỉ có 2 nồng độ của mỗi chế phẩm U₂ đại diện cho nồng độ cao
X	ln(liều)
W	hệ số dùng trong phối hợp kết quả của các định lượng độc lập (phương trình 4.2.1.-1)

[1] Vì Bảng 3.2.4.-I không có f₂ = 54, nên giá trị F tới hạn được tính bằng hàm FINV(p,f₁,f₂) của chương trình Bảng tính Excel. Có thể tính các F tới hạn khác theo cách tương tự hoặc sử dụng các bảng tra cứu chi tiết hơn.